Jak wygląda deltoid?
Jest to figura geometryczna, która posiada cztery boki. Na cztery boki deltoidu składają się dwie pary boków, które są równej długości. Z kolei dwa przeciwległe kąty znajdujące się pomiędzy bokami o różnej długości są równe. Obliczanie pola i obwodu deltoidu jest proste. Wystarczy skorzystać z powyższego kalkulatora deltoidu. Trzeba w takim przypadku znać długości boków oraz odległość pomiędzy przeciwległymi wierzchołkami. Mając takie dane obliczanie pola i objętości deltoidu będzie już tylko formalnością.
Funkcje kalkulatora
- Obliczanie pola powierzchni deltoidu – pozwoli Ci to poznać powierzchnię tej figury, co może być przydatne w wielu dziedzinach, od geometrii po architekturę.
- Obliczanie obwodu deltoidu – dowiesz się, jaka jest suma długości wszystkich jego boków, co może być istotne przy planowaniu prac budowlanych lub projektowaniu.
Jak korzystać z kalkulatora
- Podaj wymiary deltoidu: długości boków, kąty lub inne parametry, które są potrzebne do wykonania obliczeń.
- Kliknij przycisk „Oblicz”, a nasz kalkulator dokona odpowiednich obliczeń.
Dlaczego warto skorzystać z naszego kalkulatora
- Szybkość: Nasze narzędzie wykonuje obliczenia błyskawicznie, oszczędzając Twój czas.
- Łatwość obsługi: Interfejs kalkulatora jest intuicyjny i prosty w użyciu, nawet dla osób bez doświadczenia w matematyce.
- Precyzja: Dzięki naszemu kalkulatorowi możesz być pewny, że otrzymasz dokładne wyniki.
Korzystając z naszego kalkulatora deltoidu, możesz szybko i precyzyjnie wykonać różnorodne obliczenia związane z tą figury geometryczną. Daj mu szansę i przekonaj się, jak bardzo może ułatwić Twoje zadania matematyczne!
Zastosowania deltoidu w matematyce
- Deltoid w analizie matematycznej: Deltoid pojawia się w analizie matematycznej, zwłaszcza przy badaniu krzywych i ich parametryzacji. Jest używany do demonstracji różnych koncepcji związanych z krzywymi zamkniętymi i ich własnościami geometrycznymi.
- Deltoid w teorii liczb: W teorii liczb deltoid może być używany do generowania ciekawych wzorów i struktur liczbowych. Jego równania parametryczne mogą być modyfikowane w taki sposób, aby generować liczby całkowite lub inne rodzaje liczb.
Deltoid w praktyce
- Deltoid w konstrukcjach mechanicznych: W inżynierii, deltoid może być wykorzystywany w konstrukcjach mechanicznych, zwłaszcza w projektowaniu mechanizmów zmiennych ruchów. Jego charakterystyczny kształt może być używany do generowania pewnych ruchów.
- Deltoid w technologii: Deltoid pojawia się w różnych dziedzinach technologii, zwłaszcza w projektowaniu krzywych i kształtów o specyficznych parametrach. Może być używany jako element w projektowaniu kształtów np. w grafice komputerowej czy modelowaniu 3D.
Inne aspekty związane z deltoidem
- Deltoid w historii matematyki: Deltoid był obiektem zainteresowania matematyków przez wiele lat. Jego równania parametryczne zostały po raz pierwszy opisane przez francuskiego matematyka Claudiusa Richaudeau w XVIII wieku. Od tego czasu deltoid był badany przez wielu matematyków, a jego właściwości były przedmiotem różnych badań.
- Deltoid w sztuce: Deltoid, ze względu na swój unikalny i estetyczny kształt, może być stosowany w sztuce jako motyw graficzny czy element dekoracyjny. Jego geometryczne właściwości sprawiają, że jest interesującym obiektem w twórczości artystycznej.
Deltoid – wzór na pole deltoidu i obwód deltoidu
Jakie są wzory na pole i objętość deltoidu? Korzystamy z poniższych wzorów.
| Nazwa | Pole deltoidu | Obwód deltoidu | Rysunek |
|---|---|---|---|
| Deltoid | \(S = frac{|AC|*|BD|}{2}\) | \(L = a + b + c + d\) | 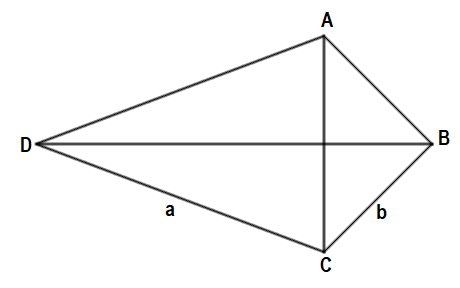 |
Ten kalkulator należy do kategorii Geometria. Możesz powrócić na stronę kategorii lub też na stronę główną portalu, gdzie znajdziesz spis wszystkich kalkulatorów.
